2024. 11. 12. 23:54ㆍ[Algorithm]/알고리즘 이론
알고리즘 개념
유니온 파인드(Union-Find) 알고리즘은 분리 집합을 관리하는 알고리즘으로
그래프 형태의 자료들의 연결 정보를 알고 싶을 때 사용된다.
이 알고리즘의 핵심 목표는 합치기(Union)와 찾기(Find) 작업을 효율적으로 수행하는 것이다.
주로 그래프에서 연결된 컴포넌트 관리 나 사이클 검출에 활용된다.
- 집합 소속 여부 판단 & 사이클 검출 : 임의의 두 노드의 연결 여부(집합 소속 여부) 확인
- 단, 무방향 그래프에서만 적용 가
- 경로 압축 : 그래프 내 노드 간의 경로 최적화
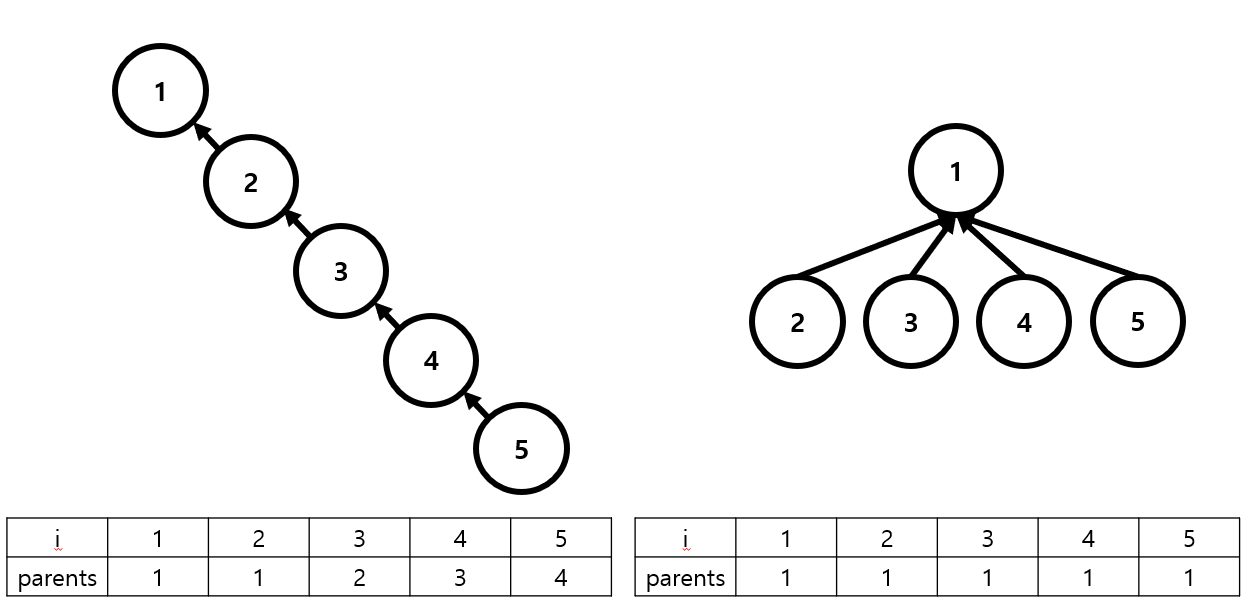
위의 경우 3과 5가 같은 그룹인지 알려면
왼쪽의 경우 자신의 부모만 기록되어 있으므로 연결여부 확인이 따로 필요하다.
이때 재귀 호출을 통해 루트 노드를 찾을 때 탐색 시간이 소요된다.
union 연산을 진행하면 루트에 바로 연결하는 것으로 인접한 부모 노드가 아니라 루트 노드의 번호를 확인할 수 있다.
이러한 과정을 통해 동일 집합 여부를 빠르게 탐색 가능하다.
알고리즘 구조
- Find: 특정 원소가 속한 집합의 대표(루트)를 찾는 연산. 각 집합을 하나의 트리 구조로 관리하면서, 각 노드가 루트 노드를 가리키도록 함.
- Union: 두 개의 집합을 하나로 합치는 연산. 보통 두 트리를 합칠 때, 한쪽 트리를 다른 쪽 트리의 루트에 붙이는 방식으로 진행.
알고리즘 흐름
1. Find
- 대상 노드 배열의 index 값과 value 값의 동일 여부 확인
- 동일하지 않을 시 value 값이 가리키는 index로 이동
- index와 value값이 같을 때 까지 재귀함수를 통해 반복
- 재귀 함수를 빠져나오면서 거치는 모든 노드 값들을 루트 노드 값으로 변경
2. Union
- 연결 할 두 노드를 find 연산을 통해 연결여부 확인
- 연결되어 있지 않다면 최적화 기법을 통해 합치기
- 랭크 기반 합치기 또는 작은 수 기준 합치기
최적화 기법
- 경로 압축(Path Compression): Find 연산을 수행할 때, 탐색한 모든 노드를 직접 루트 노드에 연결시켜 경로 압축. 이 방법은 트리의 높이를 줄여, 이후의 Find 연산을 더 빠르게 수행할 수 있음.
- 랭크 기반 합치기(Union by Rank): 두 집합을 합칠 때, 트리의 높이(랭크)가 낮은 트리를 높이가 큰 트리 아래에 붙이는 방식. 이렇게 하면 트리의 전체 높이가 줄어들어 Find 연산이 더 효율적.
두 기법을 적용하면 유니온 파인드의 시간 복잡도는 거의 상수 시간으로 최적화되며, 정확하게는 역 아커만 함수라는 매우 느리게 증가하는 함수에 비례.
시간 복잡도 분석
경로 압축과 랭크 기반 합치기를 적용하면, 유니온 파인드의 Find와 Union 연산의 시간 복잡도는 O(α(N))
여기서 α(N)은 역 아커만 함수로, 매우 느리게 증가하는 함수입니다. 따라서 실질적으로는 거의 O(1)에 가깝게 동작
코드
# 유니온 파인드 초기화
def initialize(n):
# 각 노드의 부모를 자기 자신으로 초기화
parent = [i for i in range(n)]
# 각 집합의 랭크를 1로 초기화 (rank는 트리의 높이를 의미)
rank = [1] * n
return parent, rank
# 특정 노드의 루트 노드를 찾는 함수 (경로 압축 적용)
def find(parent, x):
if parent[x] != x:
# 경로 압축: x의 부모를 루트 노드로 갱신하여 트리의 깊이를 줄임
parent[x] = find(parent, parent[x])
return parent[x]
# 두 집합을 합치는 함수 (랭크를 이용한 유니온)
def union(parent, rank, x, y):
# 각 집합의 루트 노드를 찾음
rootX = find(parent, x)
rootY = find(parent, y)
# 두 노드가 이미 같은 집합에 속해 있다면, 아무 것도 하지 않음
if rootX == rootY:
return
# 랭크를 기준으로 합침 (작은 트리를 큰 트리에 붙여 트리의 깊이를 최소화)
if rank[rootX] > rank[rootY]:
parent[rootY] = rootX
elif rank[rootX] < rank[rootY]:
parent[rootX] = rootY
else:
# 두 랭크가 같다면 한쪽에 붙이고 랭크를 1 증가
parent[rootY] = rootX
rank[rootX] += 1
참고
'[Algorithm] > 알고리즘 이론' 카테고리의 다른 글
| [Algorithm] Knapsack (0) | 2024.12.13 |
|---|